Tidens naturlære/Penduluhret
Penduluhret.
Hollænderen Christian Huyghens (Højgens), 1629—1695, havde Galilei en værdig Efterfølger paa Bevægelseslærens Omraade. Han har bl. a. Æren af at have gjort Rede for Centrifugalkraften og dens Beregning.
Ligeledes gav han Pendullæren en yderligere Afpudsning, men navnlig førte han Pendulet ind i det virkelige Liv ved at anbringe det paa Uhret isteden-for de hidtil brugte Reguleringsindretninger (S. 52). Som saadan egner nemlig Pendulet sig ganske i Særdeleshed paa Grund af sin Ligetidighed. Det gælder jo i Virkeligheden kun om at sætte et Pendul i saadan Forbindelse med et Hemværk, at dette kun kan komme 1 Tand frem for hver Svingning af Pendulet, og at hver Tand giver Pendulet et lille Tryk for at holde det i Gang. Det har mindre at sige, om Trykket er stort eller lidet. Herved vil kun bevirkes, at Svingningerne bliver store eller smaa, men det forandrer ikke noget væsentligt ved Svingningstiden og altsaa ikke ved Uhrets Gang. Saaledes bortfalder Ulæmperne ved mulige Forandringer i Loddets Vægt, Smørelse, Støv m. m.


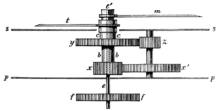
Fig. 18 viser et Penduluhrs Indretning set fra Siden, Fig. 19 bag fra. Pendulstangen U, hvis nederste Del tilligemed Klumpen er brudt af, er paa et Sted omfattet af en Gaffel T, der altsaa under Pendulets Bevægelser føres frem og tilbage tilligemed Stangen s og det paa samme Akse O siddende ankerformede Stykke NN (se navnlig Fig. 19). Hemhjulets savformede Tænder vender her udad ligesom de andre Hjuls Tænder, og Værket stræber at drive det venstre om. Paa Tegningen er dette dog hindret af Ankerhagen tilvenstre; men denne er tilligemed Pendulet paa Vej tilvenstre. Tanden slipper derfor om et Øjeblik fri, og Hjulet bevæger sig lidt frem (venstre om), men kun ganske lidt; thi N's Ankerhage tilhøjre er da naaet saa langt ind i det Tandmellemrum, hvor det allerede nu er begyndt at gaa ind i, at den næste Tand stanses og maa vente indtil Pendulet atter svinger tilhøjre tilligemed Ankeret, hvorved Hagen tilhøjre kommer saa langt ud, at Hjulet atter kan vinde en Smule frem, osv.
Paa den anden Side vil Anker og Pendul faa en lille Opmuntring ved Slutningen af hver Svingning; thi her vil Tandens Spids, idet den glider hen ad Ankerhagens skraa Flade (se den tilvenstre), saa at sige give den et lille Spark udad — som en "Tak for sidst" —, og ved disse smaa Spark holdes Pendulets Svingning let vedlige.
Det var i Aaret 1656, at Penduluhret kom til Verden. I 1657 patenterede Huyghens det, og i 1658 udgav han et lille Skrift derom. Nogle har villet frakende Huyghens Æren, idet man har fundet Pen-duluhre af adskillig tidligere Datum; men det er bleven paavist, at disse oprindelig havde været Uhre af gammel Konstruktion; men man havde senere taget Svinghjul eller Bilanz ud og sat Pendul ind i Stedet.


Der var dog en lille Unøjagtighed i det Bevis, vi (S. 63) med Galilei førte for, at Pendulsvingninger er ligetidige. Det hed nemlig, at en Sætning i Matematiken siger, at pm (Fig. 16) er omtrent 4 Gange saa lang som rm, men vi lod, som om dette var præcist. Som fin Matematiker søgte Huyghens nu at finde, hvad det er for en krum Linie, der nøjagtig har denne Egenskab, og det lykkedes ham at finde, at det er den saakaldte Hjullinie eller Kykloide. Naar en Cirkel tænkes rullende hen ad en ret Linie, vil et Punkt i Cirkelomkredsen beskrive Hjullinien (Fig. 20); men hvorledes skulde Huyghens faa et Legeme til at bevæge sig ad en saadan Bane med lige saa ringe Modstand, som et Pendul bevæger sig i en Cirkelbane? Huyghens fandt gennem matematiske Betragtninger, at dette vil ske med et Pendullegeme, naar dets Snor er anbragt imellem to Skabioner, hver formet som et Stykke Kykloide, som vist i Fig. 21, saa at Snoren skiftevis vikler sig paa og af Skabionerne for hver Svingning. Selve Pendulklumpen vil da komme til at bevæge sig i en Kykloidebane, og dens Svingninger vil blive absolut ligetidige, hvilken Størrelse end Udsvinget faar.
Nu gælder det kun om at sætte dette i Forbindelse med et Hjulværk, og dette lykkedes virkelig Huyghens, saa at Idealet var naaet: men denne Løsning er mere af teoretisk end praktisk Interesse; thi Maskineriet blev alligevel for kunstigt, og det almindelige Pendul er i Virkeligheden fuldstændig tilfredsstillende; thi det er kun en meget lille Afvigelse, der opstaar i Ligetidigheden, naar Udsvingets Størrelse forandres meget, og rent forsvindende, naar Udsvinget kun varierer lidt, hvad der just er Tilfældet paa et almindeligt Uhr.
Naar nu Pendulet bestaar af en Stang og en Klump, ligger det i Sagens Natur, at enhver lille Vægtdel af Pendulet skulde have sin egen Sving tid, alt efter dens Afstand fra Ophængningspunktet. Men selvfølgelig maa alle Delene. følges ad, idet de enes om en fælles Svingningstid. Ogsaa dette Spørgsmaal gav Huyghens en matematisk Behandling. — Der bliver aabenbart et Punkt, Svingnin-gernes Midtpunkt, der svinger paa en for det na-turlig Maade. Dele ovenfor dette maa svinge langsommere, end de vilde, hvis de bevægede sig frit. Dele nedenfor Svingningernes Midtpunkt maa svinge hurtigere, end de skulde. Er Pendulet simpelthen en i sin Ende ophængt jevn Stang, vil Svingningernes Midtpunkt ligge 1/3 fra den nederste Ende. I almindelige Penduler, hvor Klumpen er langt den tungeste, ligger det i Reglen tæt ved dennes Midte.
Et Pendul, der skal gøre en enkelt Svingning i 1 Sekund, skal have en Længde (altsaa Afstanden fra Ophængningspunktet til Svingningernes Midtpunkt) paa 0,981 Meter. Huyghens foreslog at bruge Sekundpendulets Længde som Linieenhed; men Meteren blev af Franskmændene, der har stor Fortjeneste af Jordklodens Opmaaling, taget fra disse Maalinger, og ikke fra Sekundpendulet.
Ikke mange Aar efter Penduluhrets Opfindelse blev det brugt paa en astronomisk Ekspedition til Cayenne i Sydamerika (1671—73). Det viste sig da, at Sekundpendulet ved Ækvator maatte gøres kortere end i Paris, og Huyghens paaviste, at dette hidrører fra, at Tyngdekraften bliver formindsket med Centrifugalkraften paa Grund af Jordens Omdrejning i 24 Timer. Denne havde netop Huyghens fundet paa at beregne, og den er ved Ækvator omtrent 1/300 af Tyngdekraften, saa at et Lod, som ellers vejer 300 Pund, ved Ækvator kun vejer 299 Pund, vel at mærke, naar det bliver vejet med en tilstrækkelig fin Fjedervægt. Den samme Omstændighed medfører selvfølgelig, at et Legeme ved Ækvator ikke falder saa hurtig, og at Pendulet allsaa heller ikke svinger saa hurtig som ellers. Uhret som i Paris gik rigtig, tabte i Cayenne omtrent 2 Minuter i Døgnet, saa at Pendulets Klump maatte skrues højere op; og da det herved var kommen til at gaa rigtig i Cayenne, viste det sig senere at gaa for hastig i Paris, hvor Klumpen atter maatte sænkes.
I Paris og ligeledes hos os er der dog ogsaa Centrifugalkraft; men dels befinder vi os her betydeligt nærmere ved Jordaksen, end man gør ved Ækvator (i Kristiania er Afstanden fra Jordaksen kun halvt saa stor som de ækvatoriale Egnes Afstand derfra), og dels virker Centrifugalkraften her ikke lige modsat Tyngden, men skraat, nemlig ud imod Himlens Ækvator, og dette formindsker yderligere dens Virkning hos os.
Inden Huyghens gav den rette Forklaring af, at man først i Cayenne havde maattet forkorte Pendulet og senere i Paris forlænge det, blev andre Forklaringer af dette mærkelige Fænomen forsøgt, navnlig, at det hidrørte fra Varmens Virkning paa Pendulet.
Man vidste nemlig, at en Stang bliver længere naar den opvarmes, kortere, naar den afkøles; og det var da ikke urimeligt at tænke sig, at Varmen i Cayenne forlængede Pendulet, saa at det kom til at gaa langsommere, og omvendt i Paris; men det viste sig, at denne Forklaring strakte ikke til, selv om Varmeforandringen nok har kunnet gøre noget.
Denne gør sig nemlig i Virkeligheden gældende, saa at det medfører Forandring i et Uhrs Gang, og den herved opstaaende Forstyrrelse søger man derfor at fjerne ved særegne Konstruktioner af Pendulet, de saakaldte Kompensationspenduler.

Et saadant er først opfundet af en engelsk Uhrmager John Harrison 1726. Dets Stang har megen Lighed med en Rist, idet den bestaar af 5 Stænger, Fig, 22, RTSTR, men disse er af forskellige Metaller, f. Eks. R, S og R af Jærn, T og T af Zink, og de er ikke forbundne fast med en lille Tværstang i hver Ende, men, som Figuren viser, er det kun R og R, der ophængte i den øverste lille Tværstang ab; og Midterstangen S gaar frit igennem den nederste lille Tværstang fg uden at være fæstet til denne. Derimod er de tre midterste Stænger T, S og T foroven fast forbundne med Tværstangen cd. Da nu Zink udvider sig mere end Jern, nar det opvarmes, vil Tværstangen fg ganske vist sænkes ved en Udvidelse af Jernstængerne RR; men ved den endnu større Udvidelse af Zinkstængerne TT vil Tværstangen cd løftes endnu mere, og Stængernes Længde bliver nu saaledes tilpasset, at den øverste Ende af Jernstangen S netop bliver løftet saa meget, som S udvider sig, hvorved Klumpen forbliver i samme Højde.
Man har ogsaa andre Maader at kompensere Penduler paa, f. Eks. ved at lade Klumpen bestaa
af en Cylinder med Kviksølv. Dette udvider sig med Varmen stærkere end f. Eks. Jern, og det kan da tilpasses saaledes, at skønt Pendulstangen forlænger sig, vil Svingningernes Midtpunkt dog ikke sænkes; thi det opvarmede Kviksølv naar højere op i Cylinderen.
Dersom Hemhjulet har 30 Tænder, og Pendulet er et Sekundpendul, vil Hemhjulet netop komme til at gaa en Gang rundt i et Minut. Man kan da anbringe en Sekundviser paa Forlængelsen af Hem-hjulsaksen udenfor Aksellejet. — Endvidere kan Tandantallet paa Værkets Tandhjul være saaledes tilpasset, at der er et af dem, der gaar en Gang rundt, naar Hemhjulet gaar 60 Gange. Dette Hjuls Aksels Forlængelse kan bære Minutviseren; og nu kunde de derefter følgende Tandhjul ganske vist tilpasses til, at en anden Aksel kom til at gaa en Gang rundt, naar Minutviseren gaar 12 Gange, og den kunde bære Timeviseren; men man ønsker i Reglen, at Minut og Timeviseren kommer til at dreje sig om samme Centrum, hvorved man kun faar en Uhrskive, som da tilligemed Viserne kan være forholdsvis stor. Dette opnaas ved en særlig Hjulforbindelse, som ses af Fig. 23.
e er Minutakslen, som gaar en Gang rundt i Timen, og paa hvis yderste Ende Minutviseren sidder. I et lille Rum tæt op ad Uhrskiven ss har Minutakslen en Fortykkelse b og et Hjul x med f. Eks. 10 Tænder. Dette driver et andet x' med 30 Tænder 1 Gang rundt, mens Minutakslen gaar 3 Gange rundt. Akslen for x' bærer et tredje Tandhjul z med 8 Tænder, der driver et fjerde y med 32 Tænder 1 Gang rundt for 4 af sine egne Omdrejninger, altsaa for 12 af Minutakslens Omdrejninger, altsaa i 12 Timer. Men Hjulet y er fæstet paa et Hylster c, der omslutter b, men saaledes, at det kan glide paa b, eller rettere sagt, b (med Minutviseren) gaar rundt inden i Hylsteret c uden at tage dette med sig; derimod drejes det, som paa-vist, af særlige Tandhjulsforbindelser en Gang rundt i 12 Timer, og det samme gælder Timeviseren t, som er fæstet paa samme Hylster udenfor Skiven ss.

Et Uhr, der slaar Klokkeslag, er forsynet med endnu et Værk, drevet af et særligt Lod; men istedenfor Hemhjul med Pendul, er dets hurtigst løbende Aksel forsynet med et Vindfang, der gør Modstand imod at blive drejet saa hastig rundt. Derved faar Værket et nogenlunde jevnt Løb, saa at der omtrent er lige lange Tidsmellemrum mellem hvert Skub, som en Stift paa et af Hjulene udøver paa Skaftet af en Hammer der saaledes bringes til at slaa paa en Klokke i en vis Takt. Dersom der ikke sættes en Stopper for disse Slag, vilde de vedblive, indtil Loddet var kommen helt ned; men en særlig Indretning afmaaler nu ved hvert Klokkeslet Slagenes Antal. Denne Indretning kan bestaa i en Skive, Slaaskiven, Fig. 24, hvis Rand ved Indskæringer er delt i 12 ulige store Dele. En Hage, der kan falde ind i disse Indskæringer, holder derved Skiven og Værket an; men løftes den i et Øjeblik ud, begynder Slagværket at løbe og slaar et Antal Slag, indtil Hagen atter falder ind i en Udskæring. Mellemrummet mellem Udskæringerne er nu tilpasset saaledes, at Værket kun faar slaaet 1 Slag, mens Mellemrummet 1 passerer Hagen, 2, mens 2 passerer den, osv. For hver Omdrejning af Minutviseren vil en Stift paa Minutakslen skaffe Hagen løftet ud af Indskæringen, saa at Slagværket virker, og det bliver da det nævnte Mellemrum paa Slaaskiven, der bestemmer, hvor mange Slag der skal falde.
Paa en noget lignende Maade kan et tredje Værk, Vækkeværket, træde i Virksomhed paa et ved Stillingen af en særlig Skive bestemt Klokkeslet; men her er ingen Slaaskive, saa Værket vedbliver at „vække", til det er udløbet.
Naar et Uhr er i Orden, er der ikke meget at passe derved. Optrækningen foregaar derved, at Valsen, hvorom Snoren vikles, er forbunden med det store Tandhjul, der sidder paa samme Aksel, ved en Spærhage og Spærhjul (Fig. 19) paa saadan Maade, at man med Uhrnøglen kan dreje Valsen rundt i den Retning, at Snoren paavikles, uden at det store Tandhjul tilligemed de følgende be-væger sig; men Lod og Snor kan ikke dreje Valsen rundt i modsat Retning uden at trække Tandhjul og Værk med sig, og de følger, som det er forklaret, kun langsomt med, idet Hemhjulet kun gaar 1 Tand for hver Svingning, Pendulet gør frem og tilbage.
Endvidere er der at sørge for, at Uhret bliver og forbliver ophængt saaledes, at det ikke ,,halter", det vil sige, at Pendulet faar lige stærk Impuls, naar det gaar tilhøjre og tilvenstre.
Endelig maa Pendulets Længde være rigtig tilpasset. Dersom Uhret taber, maa Klumpen skrues lidt højere op, og omvendt, hvis det vinder.
